Drawing Red Black Trees Tex

In order to get the full insight into a Red-Black Tree, I strongly suggest you read about its isometry data structure - 2-3-4 tree.

Introduction

A red-black tree $T$ is a binary search tree having following five additional properties (invariants).

1. Every node in $T$ is either red or black.
2. The root node of $T$ is black.
3. Every NULL node is black. (NULL nodes are the leaf nodes. They do not contain any keys. When we search for a key that is not present in the tree, we reach the NULL node.)
4. If a node is red, both of its children are black. This means no two nodes on a path can be red nodes.
5. Every path from a root node to a NULL node has the same number of black nodes.

Failure to preserve any of the above five properties makes $T$ a non-red-black tree. Figure 1 shows an example of a red-black tree.

The tree in figure 1 holds all the properties. Figure 2 shows a tree that is not a red-black tree.

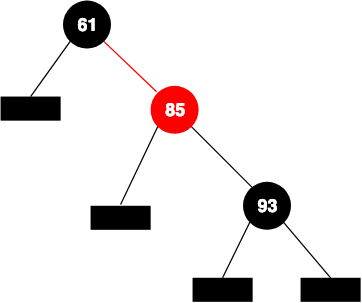
The tree in figure 2 satisfies all the invariant except invariant number 5. If you search 55 in the tree, you end up in the leftmost NULL node. In doing so, you travel through only one black node (the root node). If you search 87, you end up in the left NULL child of the node containing 93. The path has 2 black nodes. So the number of black nodes are different on a different path.

Among all the dynamic set operations (search, predecessor, successor, insert, delete, etc) supported by a red-black tree, there are two operations that may violate the invariants listed above. These two operations are - insertion and deletion. Therefore, after every insertion and deletion, we check if the operation violated any of the properties. If it did, we need to re-structure the tree to keep the invariants intact. We have three tools for this.

1. Left-Rotation: The left rotation at node $x$ makes $x$ goes down in the left direction and as a result, its right child goes up. This is illustrated in figure 3.
   

2. Right-Rotation: The right rotation at node $x$ makes $x$ goes down in the right direction and as a result, its left child goes up. This is illustrated in figure 4.
   

3. Recolor: Recolor flips the color of a node. If it is red, it becomes black and vice-versa.

We use one of these tools or a combination of them to maintain the invariants that have been violated by insertion or deletion operation.

We call the red-back tree a balanced search tree because its height is always in the order of $O(\log n)$. We can prove it as follows.

Proof:
Recall property 5 that says the number of black nodes along all paths must be the same. This means, if a tree has all the nodes black, it becomes a perfectly balanced tree. If $bh$ is the black-height of the tree, then the number of nodes in a tree where all the nodes are black is $2^{bh} - 1$. The addition of red nodes in the perfectly balanced tree increases its height. Therefore, a red-black tree of black-height $bh$ has at least $2^{bh} - 1$ nodes. The red-black tree gets maximum height when the nodes in its longest path are alternate red and black nodes. In that case, the black height of the tree is $h/2$ where $h$ is the actual height of the tree. Therefore,
$$n \ge 2^{h/2} - 1$$
Moving the 1 to the left-hand side and taking logarithms on both sides yields
$$\log_2(n + 1) \ge h/2 => h \le 2\log_2(n+1)$$

Operations

All the operations except insertion and deletion are exactly the same as the operations in the ordinary binary search tree. In this section, we discuss only these two operations. All the operations in a red-black tree take $O(\log n)$ to run.

Insertion

To insert a node $K$ into a red-black tree $T$, we do the following.

1. We insert $K$ using an ordinary BST insertion operation.
2. We color $K$ red.
3. We check if the insertion violated the red-black tree properties. If it did, we fix it.

There are several cases we need to consider. Let us suppose $P$ is a parent node, $U$ is an uncle node, $S$ is a sibling node and $G$ is a grandparent node of $K$.

Case 1: $T$ is empty.
If T is empty, we make $K$ the root of the tree and color it black.

Case 2: $P$ is black.
If $K$'s parent node $P$ is black, it can not violate any of the properties. Therefore, in this case, we do not need to do anything.

Case 3: $P$ is red.
If the parent node $P$ is red, this violates the property 4. $P$ and $K$ are now both red. The grandparent node $G$ must be black node because the tree before insertion must be a valid red-black tree. To resolve this case, we need to check whether $K$'s uncle $U$ is red or black.

Case 3.1: $P$ is red and $U$ is red too.
In this case, we flip the color of nodes $P, U$, and $G$. That means, $P$ becomes black, $U$ becomes black and, $G$ becomes red. This is illustrated in figure 5.

One thing we need to be careful in this case is when $G$ is a root of $T$. If that is the case, we do not recolor $G$ as it violates property 2.

Case 3.2: $P$ is red and $U$ is black (or NULL)
This is more complicated than case 3.1. If the uncle node $U$ is black, we need single or double tree rotations depending upon whether $K$ is a left or right child of $P$.

Case 3.2.1: $P$ is right child of $G$ and $K$ is right child of $P$.
We first perform the left-rotation at $G$ that makes $G$ the new sibling $S$ of $K$. Next, we change the color of $S$ to red and $P$ to black. Figure 6 illustrates this.

Case 3.2.2: $P$ is right child of $G$ and $K$ is left child of $P$.
In this case, we first do the right-rotation at $P$. This reduces it to the case 3.2.1. We next use the rules given in case 3.2.1 to fix the tree. This is illustrated in figure 7.

Case 3.2.3: $P$ is left child of $G$ and $K$ is left child of $P$.
This is the mirror of case 3.2.1. Therefore the solution is symmetric to the solution of case 3.2.1.

Case 3.2.4: $P$ is left child of $G$ and $K$ is right child of $P$.
This is the mirror of case 3.2.2. Therefore, the solution is symmetric to the solution of case 3.2.2.

Pseudo-code combining all these cases is given below.

RB-INSERT(T, k)
     BST-INSERT(T, k) //normal BST insertion
while k.parent.color == RED
if k.parent == k.parent.parent.right
            u = k.parent.parent.left //uncle
if u.color == RED // case 3.1
                u.color = BLACK
                k.parent.color = BLACK
                k.parent.parent.color = RED
                k = k.parent.parent
else if k == k.parent.left // case 3.3.1 and 3.3.2
                    k = k.parent
                    LEFT-ROTATE(T, k)
                k.parent.color = BLACK
                k.parent.parent.color = RED
                RIGHT-ROTATE(T, k.parent.parent)
else (same as then clause with "left" and "right" exchanged)
     T.root.color = BLACK

Deletion

The deletion operation is a bit complicated than the insertion operation. To delete a node $x$ from a red-black tree, first, we follow the ordinary BST deletion process which makes sure that $x$ is either a leaf node or has a single child. Let $S$ and $P$ are sibling and parent nodes of $x$. There are several cases of the delete operations. These are explained below.

Case 1: $x$ is a red node
In this case, we simply delete $x$ since deleting a red node doesn't violate any property.

Case 2: $x$ has a red child
We replace $x$ by its red child and change the color of the child to red. This way we retain the property 5.

Case 3: $x$ is a black node
Deleting a black node violates property 5. In order to maintain property 5, we add an extra black node to the deleted node and call it a 'double black' node. Now we need to convert this double black to a single black node. For this, we consider the following 8 cases (we discuss only four cases, the rest are just the mirror these four cases).

Case 3.1: $x$'s sibling $S$ is red
In this case, we switch the colors of $S$ and $x.parent$ and then perform the left rotation on $x.parent$. This reduces case 3.1 to case 3.2, 3.3 or 3.4.

Case 3.2: $x$'s sibling $S$ is black, and both of $S$'s children are black.

The color of $x$'s parent can be red or black. We switch the color of $S$ to red. If the color of $x$' parent is red, we change its color to black and this becomes the terminal case. Otherwise, we make $x$'s parent a new $x$ and repeat the process from case 3.1. This is illustrated in figure 9.

Case 3.3: $x$'s sibling $S$ is black, $S$'s left child is red, and $S$'s right child is black.
We can switch the colors of $S$ and its left child $S.left$ and then perform a right rotation on $w$ without violating any of the red-black properties. This transforms the tree into case 3.4. Figure 10 illustrates this.

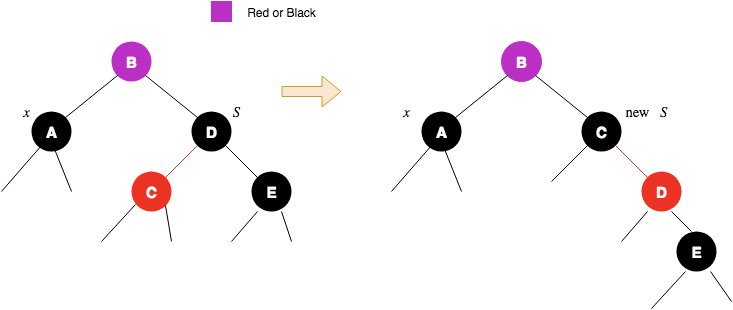
Case 3.4: $x$'s sibling $S$ is black, and $S$'s right child is red.

This is a terminal case. We change the color of $S$'s right child to black, $x$'s parent to black and perform the left rotation $x$' parent node. This way we remove the extra black node on $x$. This is illustrated in figure 11.

Let us combine all these cases to make a pseudo-code for deletion.

RB-DELETE(T, x)
     BST-DELETE(T, x)
while x $\ne$ T.root and x.color == BLACK
if x == x.parent.left
             s = x.parent.right
if s.color == RED
                 s.color = BLACK // case 3.1
                 x.parent.color = RED // case 3.1
                 LEFT-ROTATE(T, x.parent) // case 3.1
                 s = x.parent.right // case 3.1
if s.left.color == BLACK and s.right.color == BLACK
                 s.color = RED // case 3.2
                 x = x.parent //case 3.2
else if s.right.color == BLACK
                     s.left.color = BLACK // case 3.3
                     s.color = RED //case 3.3
                     RIGHT-ROTATE(T, s) // case 3.3
                     s = x.parent.right // case 3.3
                 s.color = x.parent.right // case 3.4
                 x.parent.color = BLACK // case 3.4
                 s.right.color = BLACK // case 3.4
                 LEFT-ROTATE(T, x.parent) // case 3.4
                 x = T.root
else (same as then close with "right" and "left" exchanged)
     x.color = BLACK

Implementation

I have implemented the Red-Black tree is C++, Java, and Python. Some of the extreme cases are not tested. In addition, I first wrote the program in C++ and simply converted it to Java and Python code. Even though they normally work, the implementations (java and python) may not work in some situations. Please find the source code on Github.

C++	Java	Python
Click Here	Click Here	Click Here

References

1. Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (n.d.). Introduction to algorithms (3rd ed.). The MIT Press.
2. Red Black Tree Deletion. https://www.youtube.com/watch?v=CTvfzU_uNKE

valtierrautmacksmay.blogspot.com

Source: https://algorithmtutor.com/Data-Structures/Tree/Red-Black-Trees/

Share this post